Introduction
The use of regression analysis in applied problems has a distinct advantage because it allows us to predict the relationship between the variables under study. This report examines the relationship between the average age of the aircraft fleet and direct maintenance costs. The essence of this examination is the reorganization of North-South Airlines (NSA) and the desire to provide increased operational performance following the merger of Northern Airlines (NA) and Southeast Airlines (SA). The parent companies differentially provided maintenance costs for their respective fleets, so there is a need for NSA to create a regression model to predict the relationship between aircraft life and direct costs. Examining this relationship will allow Stephen Ruth to make strategic decisions associated with aircraft maintenance costs at a newly formed airline.
Analysis
One of the main characteristics of airline reliability that determines the need for direct maintenance expenditures is the life of the aircraft. The longer an airplane has been in service, the more worn out its parts become; potentially leading to breakdowns and plane crashes that cause severe damage to the business (Brown, 2021). In order to avoid this outcome, companies increase maintenance costs based on the belief expressed in the scenario that the older the aircraft, the more investment it requires. In the case study, the NSA inherited fleets from two merged companies, NA and SA— in which case the NSA finds itself in a deliberately difficult position because it received aircraft already in service with different useful lives. Noteworthy, Stephen Ruth, as the new president of the company, is interested in improving NSA’s operational efficiency by scrutinizing the cost structure of the aircraft. In this case, a regression analysis should be conducted to test the hypothesis stated.
The choice of a regression model to analyze the data is not accidental but instead comes from the applied nature of the task. More specifically, Stephen Ruth’s request examines the relationship between two variables, the average age of the fleet for a given year and the cost of maintenance. It should be said that the regression model tests what effect the independent variable (age) has on the dependent factor (cost) — it is important to point out that this relationship can be either increasing or decreasing (Kumari & Yadav, 2018). The point of regression comes down to testing the statistical significance of the null hypothesis postulating the absence of this relationship. In particular, the basic linear regression model for one independent variable is shown in the equation [1]. In this equation, according to the null hypothesis, β1=0, which means there is no relationship between Y and X. The regression model also operates the coefficient of determination, which determines the overall reliability of the calculated model (Rao, 2020; Chicco et al., 2021). The closer this parameter is to 1, the more dependable the model is.
Y = β0 + β1X
Solution
MS Excel was used to design a linear regression, which allows to automatically calculate not only the regression coefficients and the coefficient of determination but also the corresponding p-value to test the statistical hypothesis that there is no relationship. Two relationships between variables were tested for two companies each, namely, age as an independent factor of influence on airframe and engine costs. Regression analysis data were obtained for NA, shown in Table 1. It can clearly be seen that statistically significant regression models were only found for NA, for which the age of the aircraft has been shown to have an effect on airframe and engine costs. Notably, airframe and engine costs increased at about the same rate as a function of age in NA. It is worth noting that the coefficient of determination for the “age/airframe costs” pair was on average 25.7% higher than for “age/engine costs.” This says nothing about causality but only indicates that the first model satisfies the variance of all data better than the second. In addition, at the zero point — when aircraft age is zero — it is assumed that airframe costs appear to be one and a half times higher than engine costs, based on Table 1.
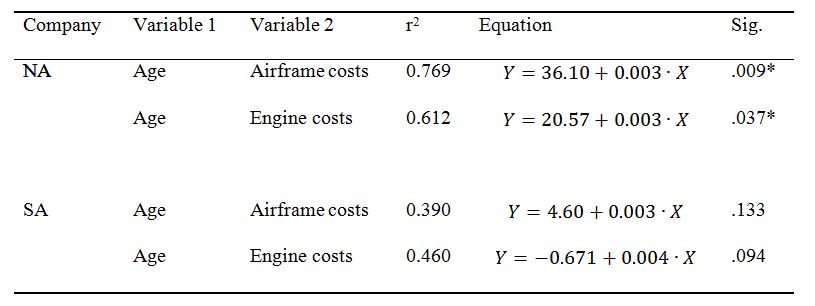
On the other hand, statistical significance was not found for relationships in SA: meaning that there is not enough reliable evidence to support that there is a relationship between fleet age and direct maintenance costs. However, the test conducted is still ambiguous about the relationship between the variables, as small sample size or lack of a linear relationship may be to blame for the statistical insignificance (Ebert, 2018). In other words, there is a need to refine the test results.
Justification
Since the purpose of the analysis was to test the relationship between average fleet age and direct maintenance costs, linear regression is ideal for this purpose. The statistical analysis performed was able to answer the central question of whether such a relationship exists. It was shown that for NA, increasing the age of the aircraft results in higher airframe and engine costs. Specifically, each additional hour of operation increases this parameter by $0.003. It should be noted that there was no statistically significant relationship between the variables for SA, and this also confirms Stephen Ruth’s concerns about the parent companies’ differential approaches to cost management. A possible reason for the lack of a statistically significant relationship for SA could be the newer fleet: on average, the age of the SA fleet is 1.65 times lower. As a result of this difference, costs may not be linearly or at all related to age, requiring a closer analysis of the spending agenda in SA (Sharma, 2022). Because the NSA received aircraft fleets from two companies at once, the NSA resources ended up with aircraft simultaneously showing and not showing regression significance for these variables. Therefore, a unified reorganization system should be developed to treat the aircraft from the parent companies as a single, connected network.
Conclusion
This report examined the regression relationship between fleet age and maintenance costs. The general idea was that as maintenance costs increase, so do maintenance costs. This leads to higher operating costs in the company and reduces operational efficiency, although it increases reliability. This relationship was confirmed for the parent company NA but not confirmed for SA. Based on this, there are two different solutions. First, the NSA needs to develop a unified aircraft registration system to create a unified network. Second, a more detailed analysis of the SA fleet needs to be conducted, and possible reasons for the statistical significance disruption explored.
References
Brown, J. R. (2021). 4 reasons why airlines are always struggling. Investopedia. Web.
Chicco, D., Warrens, M. J., & Jurman, G. (2021). The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Computer Science, 7, 1-24. Web.
Ebert, T. A. (2018). Why regression coefficients are not statistically significant in simple regression. ResearchGate. Web.
Kumari, K., & Yadav, S. (2018). Linear regression analysis study. Journal of the practice of Cardiovascular Sciences, 4(1), 33-36. Web.
Rao, K. (2020). r² or R² — when to use what. TDS. Web.
Sharma, P. (2022). Different types of regression models. Analytics Vidhya. Web.
